Picture this. It's the first term of your first year and you think you've finally got all your courses worked out. But alas, you open myUNSW and realise you still have to choose the actual classes you're in! Surely there's no way you're bothered to compare all the classes for all your courses. Turning to Google, you discover UNSW has not one, but two timetable planning applications, each with their own autotimetabling feature to help you make a timetable that fits your schedule.

Notangles, https://notangles.csesoc.app/, is a beautiful timetabling app that streamlines the class scheduling experience. It caters towards all faculties in UNSW, and has additional features such as auto-timetabling, custom events, and most importantly, light to dark mode.

Meet the Competition 🤔

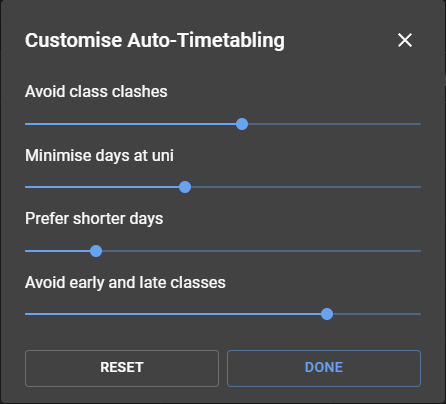
CrossAngles uses a weighting system to determine the most optimal timetable. The weights of each category can be adjusted using these label-less sliders, with the total of the weights being a constant. Unfortunately, the user has no idea exactly what these arbitrary sliders mean unless they peek into the source code (which can be found here).

I can, however, attest that their algorithm does work - this timetable was automatically generated after maxing out the 'minimise days at uni' setting. I didn't even have to manually run the algorithm - the classes moved by themselves after I got rid of the lectures.

The Premier Solution 💪

Notangles had previously tried to roll our own auto-timetabling algorithm too, but to no avail. Thus, we decided to employ the assistance of Google's OR-Tools library, designed specifically for optimisation problems like timetable scheduling. To be more precise, timetables fall into the category of Constraint Optimisation, where the solver is given several constraints, such as which days you would like to go to uni, and create at least one solution that satisfies all the provided constraints. It may not be the best solution, but it doesn't matter. All that matters is that the constraints were satisfied.

The Model

The first step in generating a valid timetable is defining a model, the representation of a problem, which should have all the info a solver needs to solve a problem. As a part of this model in this case, various types of variables are defined to represent classes in a timetable.

Firstly, integer variables are used to represent what times each class starts. An integer variable is a variable which can only take certain numerical values. We define these possible values as the starting times of all the periods.

Next, interval variables are used to represent during what times the classes occur. An interval variable is a variable that, in our case, represents a fixed interval of time - the length of a class plus the "breaks between classes" amount (in hours). By telling the solver to make these intervals never overlap, we can generate a timetable with no clashes! These intervals are also used to constrain the "earliest start time" and "latest end time" constraints - we simply added an interval to the model which started from the start of the day to the earliest start time and vice versa for the end time - in essence, pretending a class exists during that time.

So far, this covers the simple classes which occur once a week. For classes which are made out of two consecutive periods, like tut-labs, we can simply reduce them down to a single long class with one start time and one interval. But what about classes which are linked across different days, such as lectures? We can't use integer variables or integer variables directly since these classes must be represented with arrays.

This is where our third type of variables come in - boolean variables. A boolean variable is exactly as its name suggests - it can only take the values 1 or 0, i.e. True or False. By associating a boolean variable with each possible set of grouped classes, the solver effectively switches each one on or off to see if they fit the current constraints. We can further constrain only one of these boolean variables to be switched on at any given time, to ensure that only one lecture slot is chosen.

Now that we have determined how to arrange classes in such a way that they both fit the timetable data provided and never clash, we must now deal with the user's preferences.

An Aside: Data Representation

Before we move on, a quick aside to explain how the timetable data is encoded. Taking a step back from the whole timetable side of things, a constraint optimisation problem can be thought of as a way to find integer solutions to a set of linear equations (apologies to anyone whose wounds are still raw from their maths exams). Applying this notion to our problem, we need to be able to concisely express when a class starts in an integer format. We did this by encoding every start time as a three digit number - the first digit is the day of the week (with Monday as 1) and the remaining two digits are the hour, multiplied by two to remove those pesky decimal points. Namely, class_time = day_of_week * 100 + start_time * 2. A class's duration must likewise be multiplied by two as well, to deal with classes ending on the half-hour. This does assume that all classes either start/end on the hour or on the half-hour - we have not found a class that behaves otherwise yet, but if there exists one please let us know!

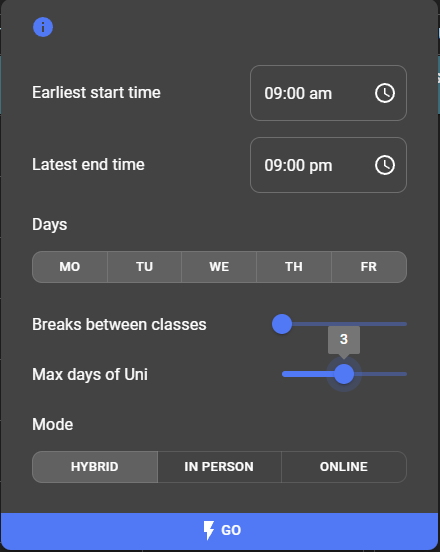
More Constraints

Back to constraints. As mentioned before, the "earliest start time" and "latest end time" constraints are dealt with by pretending a class exists ending at/starting from those times respectively, and the "breaks between classes" constraint is simply an extra number of hours added on to the length of each class. The "mode" is handled by filtering the classes by their teaching mode. But for the days of the week and the "max days of uni" constraints, we must bring back our friend the interval variable.

To represent the days classes can be scheduled, we can use an integer variable that has a domain of precisely those days. Then, we can add a constraint that class_time // 100 == class_day_time to weed out any classes which do not match the specified days. The process for maximum days is similar - we declare an array of n integer variables that represent the n number of days you want to go to uni. Now we can simply ensure that every class's day corresponds to one of these integer variables. Recall that integer variables can only be associated with a single value. So for example, if classes fell on days 1, 2 and 3, but we only had two integer variables to represent a maximum of two days at uni, one of these classes (it doesn't matter which one) would not correspond to any of the variables! Hence, the constraint cannot be satisfied.

Finally, to get the actual result, we also have to associate each specified constraint with a boolean variable representing whether the constraint is enforced or not. This is so that we can tell the solver to maximise the sum of these boolean variables, hence maximising the number of constraints we enforce, and by extension satisfy, on the timetable data. We have defined that there can only be a maximum of three constraints that are not satisfied before the solution is considered imperfect.

And voilà! Using this model, the solver can now generate all the timetables which fit the given criteria. We then return the first solution to the user via our gRPC server, since all of them are valid anyway. All this with just under 300 lines of Python code.