Circling Degree Plans: Teaching Computers How to Read

alternatively, "Fighting UNSW's Handbook"

Reading is something that humans usually “pick up”. After learning the fundamental building blocks – the alphabet, punctuation, basic word structure – and you may have been able to pick up a certain level of reading comprehension from watching a teacher, or parent, or sibling read. Computers are pretty different in this regard, since learning is hard, "picking up stuff" is hard, and doing all of that in the time-limit expected by users,as small as milliseconds, is very hard.

Let’s take a look at Circles, our degree planning app:

As soon as we start thinking about making this app, we are immediately hit by our first problem - how do we make computers understand our handbook, which is designed for humans to read?

The challenge

To achieve our goal of providing these warnings to the user if they misplace a course, we would want to convert course requirements from the UNSW Handbook into something we can check programmatically.

In other words, we want to convert something like:

into a function which accepts a user's degree plan and marks, and returns whether or not they can do that course. For example, if person A hasn’t done COMP2521 or COMP1927 for this prerequisite then it’ll return False, but if person B has done COMP2521, and gotten a credit, then it’ll return True.

Note, we need to do this process for all courses. Our initial temptation is to use brute force – we write a function for each course manually – but this will then need a human to intervene for every course! Imagine doing this for the 1,000 courses that are already on the Handbook. Worse, we would have to edit these functions every time a new course is created or edited, and yes, that is as painful as it sounds. What we need to do is find a way to convert these prerequisite instructions into code automatically, to cut down on the ridiculous number of human hours this method demands.

Remember though, that the prerequisites are basically written in English. This is easy enough for a human to understand - which is why we were tempted to do our first solution. We are left with a fundamental problem - is it possible to parse these human, English instructions and allow machines to understand them? The answer to this, looking at CS theory, is a resounding no.

An easy-to-understand example of why this isn’t possible is based around ambiguous grammar. We see this in our prerequisite string at the beginning of this section:

Does the "mark of 65" apply to both 1927 and 2521? Or does taking 2521 mean that you can just pass the course, while 1927 students must get a credit?

The Handbook is ambiguous, and uses this exact phrasing to mean either what’s highlighted in red or what's highlighted in green. I can only tell you that the right answer here is the one in red by knowing that COMP1927 was the old course code for COMP2521, which is not immediately obvious without having extra knowledge.

So, we seem to be at a standstill. How can we make a general solution that applies to all courses?

As every good CS student does when confronted with an impossible problem, we first need to look carefully at the task we have to do, look for patterns and break down the problem to make it easier. We can actually see that there is a pattern in how these strings are constructed - there is usually a list of conditions joined by AND or OR, and those conditions are mostly repeated phrases like:

• Prerequisite: ACTL1101 AND (MATH1251 or MATH1241)
• Prerequisite: (MATH2501 or MATH2601) and (MATH2011 or MATH2111) and (MATH2801 or MATH2901)
• Prerequisite: ACTL2101 and enrolment in program 3587
• Prerequisite: a mark of at least 70 in COMP3511 and a mark of at least 65 in COMP2511
• Prerequisite: A mark of at least 65 in COMP1927 or COMP2521

After collecting the basic components – course codes for prerequisites, marks, UoC, and others – we can get our computer to comprehend more complex prerequisites in our handbook by understanding how these basic phrases are grouped together.

After a bit of thinking, we found that this problem is actually something that computer scientists have run into before. We want to convert some input - which is semi-structured - into a more ordered instruction set for computation. We then want to abstract away some of the complexities of a human-readable instruction set and handle it through some sort of translation layer instead.

We have to make… a compiler.

Compiling the handbook

Here’s our example again:

Since English is ambiguous and hard for our machine to understand, we want to get rid of as much English as possible. We use regexes (Regular Expressions - which are a powerful way of manipulating strings) to do this - however, because English is not a regular language, we can't use only regexes to parse the whole handbook. James Ji covers in more detail what a pain that all is in a showcase he did in 2021.

Once we clean up all the messy ambiguities and typos, we obtain something that’s more standardised, which is what I’m going to focus on:

From this cleaned-up prerequisite, which you can think of as our own Handbook “language”, the real compilation starts.

Parsing

Here, we will consume all our tokens to produce an abstract syntax tree (AST). This is basically a way to structure our prerequisite in a way a machine can better understand. For example, A human can read:

as “if I have already done COMP6969 I can stop reading, but otherwise I should do COMP1521 and COMP2521”. An AST basically uses a tree structure to spell this out for the computer, which would look something like this:

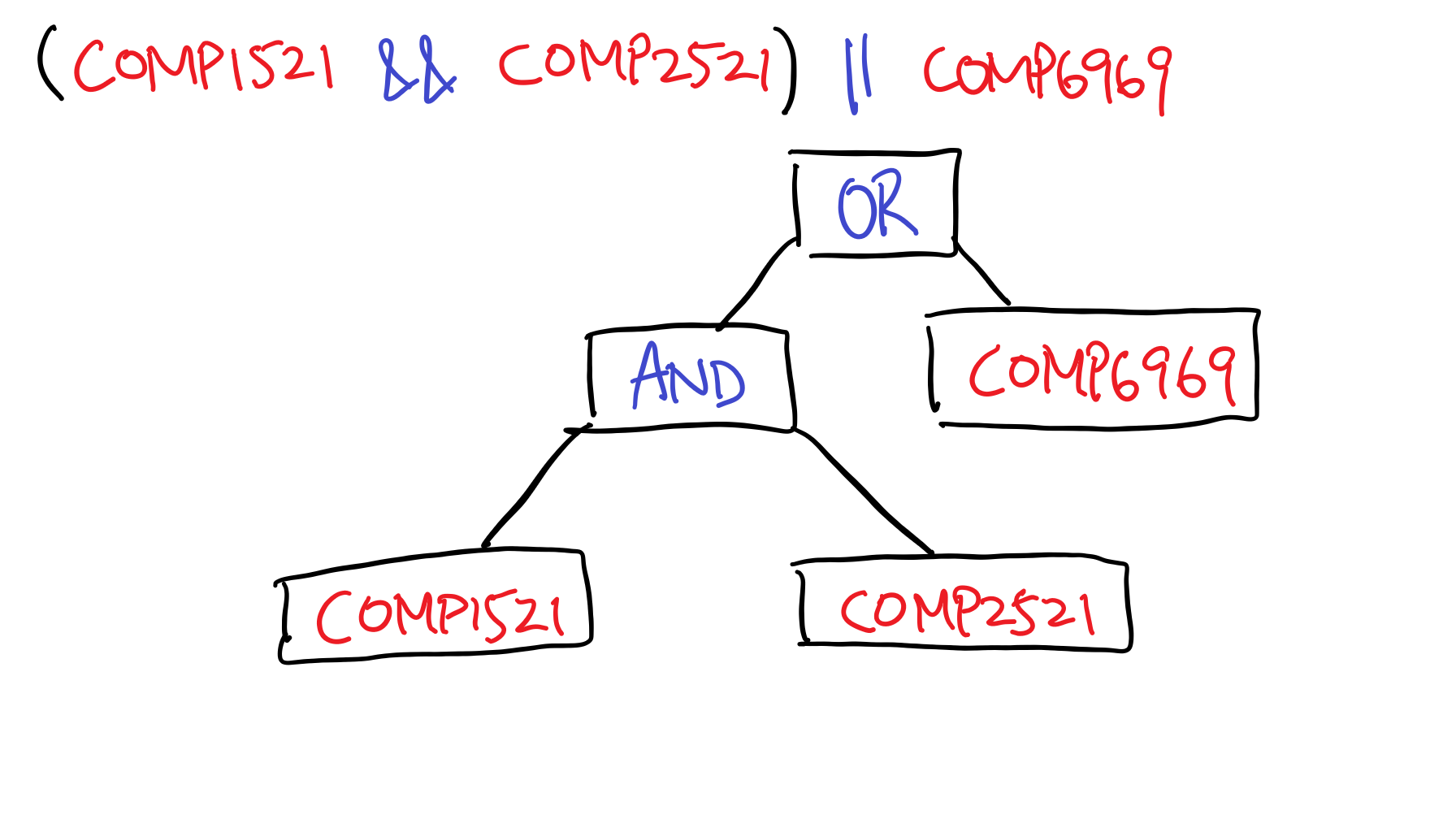
You might be wondering, “what was the point of drawing up a tree when I can read the prereq in the exact same way”? The important thing to understand is that computers see the same things we do – the course COMP1521, the “&&” symbol and the parentheses – but they don’t know what any of those key phrases (tokens) mean.

By converting it to an abstract syntax tree, computers would have an easier time comprehending those tokens – it now knows, for example, that the “AND” has two arguments, COMP1521 and COMP2521, and we can do further processing from there.

We have the "tree" bit, now we should explain what the “abstract syntax” in AST means in Circles. This will actually be the way we can do something with this tree. For this, Circles defines a Condition and a Category.

A condition is something we can decide to be True or False using a method, which we will call "validate". This is the function that we were talking about at the start of the article that says whether or not we can do a course!

This can be a simple operation or a complex one. It is simple in the case of a single course - we look through the user and see if the course is completed by the user. It gets more complex in the case of a composite condition like an AndCondition, which contains other conditions inside it which have to be compared. In that case, we would need to run the "validation" for every condition, then return a single value if it was all valid - else we return false.

A category is simpler. It is a filter which decides whether or not a course fits into the category, using a definition. We can use this higher order function to, for example, filter the courses the user has taken by using a function which only allows maths courses. After this, we can decide if the user has completed enough courses to do MATH3231, which requires 12 UOC of level 2 maths.

Tying everything together, to create the validator for our course itself, Circles uses the function create_condition:

def create_condition(tokens) -> Tuple[Condition | None, int]:

This function will return two things:

1. if the Condition is successfully created, it will be returned, otherwise, we will return None. if we can't confidently say what the string reads, we should default to saying nothing at all.
2. an integer indicating which token our function failed at, if any.

Doing this enough times, we have the ability to generate an AST, filled with Conditions, from our English text. By using the .validate method on each Condition, we have what is known as an attribute grammar for our tree.

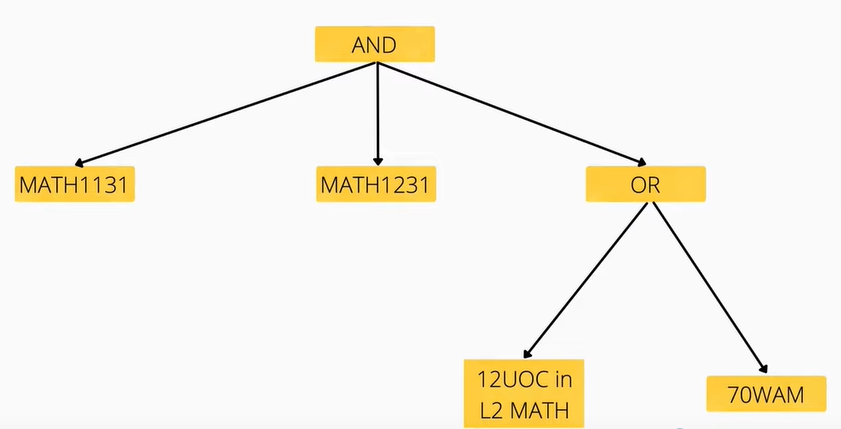
Here is a more complicated tree, taken from James's presentation:

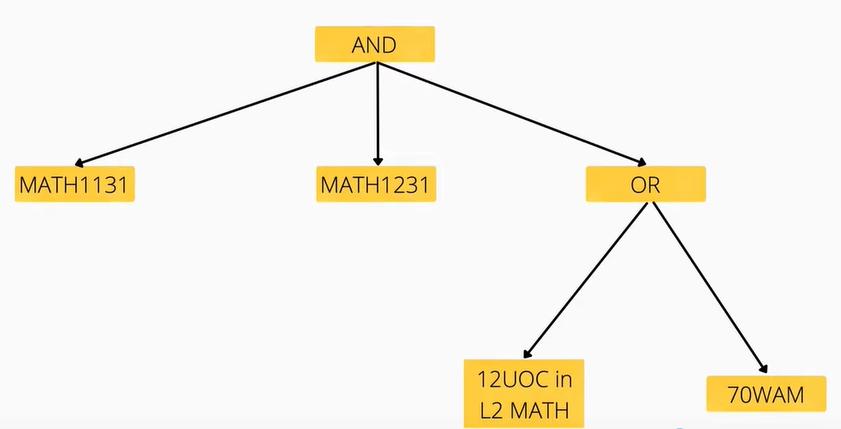
An attribute grammar is essentially what is already done through the "validation" function - it simply traverses the tree and follows predefined rules to synthesise a result. Let's take the "OR" section on the bottom-right of the tree above, for example:

• If we see OR, evaluate to True if one of the leaf nodes is True.
• If we see 70WAM, evaluate to true if our user has a 70WAM.
• If we see 12UOC in L2 MATH, evaluate to true if we (the user) have 12UOC completed in the "Category" of Level 2 Maths. This category is defined as a course code of the form MATH2XXX.

Following the logic above, if a user has a WAM of 68 and completed both MATH2069 and MATH2521:

• At the OR, we check the two leaf nodes, 70WAM and the 12UOC requirement.
• Our user has a WAM lower than 70, so the 70WAM node is False.
• However, our user has completed two Level 2 Maths courses, so the 12UOC node is True.
• Because one of the child nodes is True, then we've satisfied the condition of 70WAM || 12UOC in L2 MATH.

We can also define other attribute grammars, which you can look at if you check out the Circles repo and check out the full definition of a Condition. Every single method on Condition actually defines an attribute grammar on this AST.

So, with that, we are done! After we make our AST and define our categories and conditions, we obtain a way to process our language.

Conclusion

We can see that the 30 seconds you took to process a course prerequisite were a small fraction of the time it took us to solve this problem 😁. This may seem disproportionate — but such is what CS is all about. After all, why spend 30 mins doing something when it can be automated in 100 hours(?) But for one, thousands of students now don’t have to spend those 30 minutes looking up Handbook entries, and I think what is more valuable is the cool stuff like compiler theory and architecture that this problem led to.

Now, if you have used Circles before or have thought about the implications of this a bit more, you may notice that there are still a few interesting things still not covered. For example: if we can automate the decision-making of whether or not a degree is valid, then given a list of courses, I should be able to automatically arrange them in a valid order for you! That is, given I have a user that is really keen to do CS with all the security courses, I can tell them the best way to arrange their courses so that they graduate on time.

Since I have validators, I can at least achieve this by brute force by having all possible combinations of courses in terms and seeing which ones don’t violate prerequisites. However, like what we’ve seen in our journey to teach computers how to read, the world of CS can give us insights into doing this in a smart way 👀.